| Physical Principles: Conservation of Energy. |
| Student Prerequisites: For this demonstration, students need to be familiar with the following concepts - a.) the definitions of potential and kinetic energy in Classical mechanics, and how they tie into the Principle of Conservation of Energy, and b.) the concept of centripetal force and centripetal acceleration for a body undergoing uniform circular motion. |
| Introduction: The Principle of Conservation of Energy applied to a Loop - the - loop setup enables the calculation of the minimum height from which an object needs to be released, so that it may negotiate the loop without losing contact.
In this experiment, students will combine their knowledge of the Principle of Conservation of Energy and the concept of Centripetal Force as a resultant force in circular motion to predict a simple expression for the speed of the object at the highest point on the loop. It will be seen that for objects that involve rotational motion (such as the steel ball used in this demonstration), rotational kinetic energy plays a significant part in determining the height from which the ball should be released so that it stays on the track without losing contact.
The primary objective of this interactive demonstration is to convince students of the fact that physical processes seldom work in isolation, so that by correctly identifying and "breaking up" a process into its sub - processes, fundamental laws may be combined to make simple, yet elegant predictions about the behavior of one or more properties of the system.
|
Description of the Demo: At the bottom of the ramp, the potential energy of the ball gets converted into translational and rotational kinetic energy. Thus, for a ball of mass m with speed vb at the bottom of the ramp, conservation of energy yields:
Utop = Kbottom
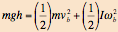
Students may be reminded that an object exhibiting uniform circular motion experiences a force directed toward the center of the circle (centripetal force), and in fact, this is the net force acting on the object . Thus, if the ball has speed vt at the highest point of the loop:
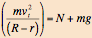
If the ball is to negotiate the loop without losing contact with the track at any point, it needs a certain minimum speed as it enters the loop. This speed may be found from the condition when the ball loses contact with the track at the top of the loop, i.e., by setting the normal force to zero in equation (2) above.
The right hand side of equation (1) can be reduced to an expression in terms of m and vb alone,if the appropriate substitutions are made in the second (rotational) term for I and the angular speed (which is linearly related to the translational speed).The minimum kinetic energy that the ball requires as it enters the loop is the sum of the kinetic energy at the highest point of the loop, and the potential energy gained in getting to the highest point in the loop (where the reference level for potential energy is chosen to pass through the center of the ball at the bottom of the loop). From this, the minimum speed required to complete the loop as the ball enters it can be found.
Finally, the minimum height from which the ball needs to be released from rest on the ramp can be found by substituting the value of this minimum speed found above into equation (1).
|
| Instructions: If friction is ignored, and all of the kinetic energy of the ball is assumed to be translational, the minimum height of release on the ramp turns out to be considerably less than the case when the effect of friction (manifest as combined translational and rotational motion) is included. Students can be made to predict the minimum height of release in each case, and shown that in the former case, the ball fails to complete the loop, while the latter calculation yields a much more accurate prediction.

|
| Notes to the Instructor: 1.) Since the radius of the ball is not negigible, the radius used in the expression for centripetal force is actually the effective radius of the center of mass of the ball on the loop, i.e., the difference between the radius of the loop and the radius of the ball. 2.) The height of the track needs to be taken into account when measuring the height of release on the ramp above the base of the setup. |
| Possible CPS Questions:
1. What is the speed of the ball at the bottom of the ramp...? [Question] [Answer]
2. Below what speed will the ball lose contact with the track...? [Question] [Answer]
3. What is the minimum K.E. required so that the ball stays on the track...? [Question] [Answer]
4. What is the minimum height from which the ball should be released...? [Question] [Answer]
5. Taking into account the effect of friction, what is the speed of the ball at the bottom of the ramp...? [Question] [Answer]
6. Taking into account the effect of friction, what is the minimum height from which the ball should be released...? [Question] [Answer]
|
|
|