Physical Principles: Components of vectors and vector addition |
Student Prerequisites: For this demonstration, students need to be familiar with the
following concepts - a.) triangulation, b.) two-dimensional vector
addition, c.) resolution of a two-dimensional vector into components
along perpendicular axes, d.) conditions of equilibrum, and e.) mass and
weight. |
Introduction: The mathematical description of resolution of forces
demonstrates the usage of vectors in dealing with physical quantities
involving more than one dimension. In this demo, we attempt to verify the
vector addition of forces through a two-dimensional case. Students will
apply their knowledge of trigonometry and rules of vector operations to
make quantitative predictions about forces on two spring scales, and
thereby to make comparison and convince themselves.
The primary objective of this
interactive demonstration is to help students comprehend the vectorial
nature of forces as well as basic properties of vectors as a
multi-dimensional generalization of scalars in characterizing physical
quantities with directions. Under this consideration, multi-dimensional
vector additions can be simply reduced to compositions of handy
one-dimensional scalar additions along corresponding directions, each of
which can be treated separately. |
Description of the Demo: Our setup consists of two spring balancing hung with a mass
suspended off center between them. The whole system should be kept in a
stationary state so that the condition of equilibrium can be applied:
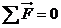
... (1)
or specifically in component form:
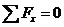 , , 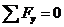 . .
... (2)
There exists certain ambiguity
student should be aware of in choosing a certain rectangular coordinate
system to perform the resolution. For example, we may have horizontal
x-axis and vertical y-axis with the origin located at the hanging point C
(see picture below). As we know that components of a vector can be
treated as one-dimensional scalars along respective directions, component
equations (2) therefore can be embodied with consideration of geometrical
relations. Students may also be asked to establish their own coordinate
systems to carry out the resolution. Generally, we want to obtain such a
coordinate system that calculation on it may be simplified.
We need to assume that the weight of
either spring scale (and of course rope) is negligible and thus the
scales and ropes and beam can be viewed as forming a perfect triangle
denoted by 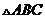 (see
picture below). Given that (see
picture below). Given that
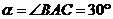 , , 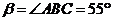 , ,
... (3)
and that the weight we use is
2kg, students then may
be required to work out explicit expressions of (2) and give numerical
results. |
Instructions: The ropes with knots on both ends have been prepared in
proper lengths to give 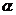 and and 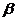 the values
in (3). Ideally, these angles can also be observed from protractors.
However, for a reason mentioned below, sole reliance on protractors to obtain
these angles is definitely not recommended. the values
in (3). Ideally, these angles can also be observed from protractors.
However, for a reason mentioned below, sole reliance on protractors to obtain
these angles is definitely not recommended.
As always, the whole setting should
be kept still before the spring scales are read.

|
Note to the Instructor: 1.) In practice, the protractors giving angles here unfortunately
can only be used as coarse reference, because the scale disks not only
block the view but also deflect ropes by their weights which make it
impossible to obtain precise readings. One may consider switching the
scale with the rope attached to get a better view of protractors, however
if doing so, the weights of scales would cause increasing error which turns
out somewhat intolerable, as has been practically observed. If students
insist, this inadequacy may be partially cured by providing the actual
lengths of three edges listed as following:
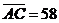 , , 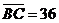 , and , and 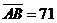 all in
inch; all in
inch;
or in more detail, the length of the
scale when stretched being approximately 18 inches together with the left
rope 40 inches and the right rope 18 inches. One can verify that these
lengths yield the angles we need. 2.) Dedicated setup time may be
required. |
Possible CPS Questions:
1. Are
tensions equal along the two ropes tied up at point C as in the picture?
[Question] [Answer]
2. Which of the following coordinate systems
can in principle be used for resolution of forces? [Question] [Answer]
3. Will resolutions in different applicable
coordinate systems give the same result of prediction? [Question] [Answer]
4. Based on Question 2 and 3, choose your coordinate
system to predict the readings of both spring scales… [Question] [Answer]
5. What effect does
changing the mass of the weight have on the readings of both scales? [Question] [Answer] |
|
Page created by
Xuefeng Zhang, Dept. of Physics & Astronomy, University of New Mexico |