Physical Principles: Wave motion, wave interference and boundary conditions |
Student Prerequisites: For this demonstration, students need to be familiar with the
following concepts - a.) periodic transverse wave, b.) wave speed, c.)
wave function for a sinusoidal wave, d.) one-dimension wave equations
with boundary conditions, and e.) wave interference. |
Introduction: Wave phenomena can occur whenever a system of continuous
medium is disturbed from equilibrium and when the disturbance with energy
can travel, or propagate, from one region of the system to another. A
general description can be given by wave equation with wave speed
determined by medium. One important special case of sinusoidal waves is
the pattern of a repeating sine or cosine function, which, however, can
construct complicated wave patterns by overlapping.
In this experiment of wave tables,
students will be asked to make qualitative or semi-quantitative
predictions about 1.) wave speed dependence on the medium, 2.)
overlapping of different waves, 3.) shapes of standing waves and
reflected waves, and etc.
The primary objective of this demonstration
is to show various apsects of wave motion to students, such as wave
pulses, sinusoidal waves, wave speed, standing waves and reflected waves.
By examining corresponding consequence of wave equations with these
phenomena, students should be able to appreciate the formailsm of wave
equations as the valid general mathematical description of wave motion,
as well as the principle of superposition due to the linearity. |
Description of the Demo: Our setup consists of a stiff steel wire with a square
section along which long iron rods with their tips highlighted are
attached at regular interval and at right angles. In this way, the shear
strain of the wire spine is amplified and becomes visible. If we tip the
first rod, a torsion wave will travel steadily down the spine. In
particular, if we generate a sinusoidal wave, every rod will oscillate up
and down about its equilibrium position with simple harmonic motion. Two
such tables are shown below. Note that the black wave table has a portion
of shorter transverse rods than the red wave table.
Wave equation reads:
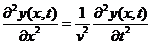 , ,
... (1)
where a disturbance can propagate as
a wave along the 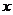 -axis with wave speed -axis with wave speed 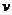 . The wave function . The wave function 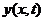 being
sinusoidal is not needed. In general, wave speed is determined by
mechanical properties of the medium. Remarkably, the speeds of many kinds
of mechanical waves turn out to have the same basic mathematical
expression: being
sinusoidal is not needed. In general, wave speed is determined by
mechanical properties of the medium. Remarkably, the speeds of many kinds
of mechanical waves turn out to have the same basic mathematical
expression:
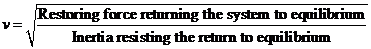 ; ;
... (2)
for the example of waves on a string,
given the tension 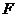 in the
string and its mass per unit length in the
string and its mass per unit length 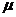 (linear
mass density), one has the wave speed (linear
mass density), one has the wave speed 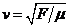 . One essential property of Equation (1) is the
linearity, which basically means that the algebraic sum of two wave
functions is again a valid wave function subjected to Equation (1). This
property is also called the principle of superposition. . One essential property of Equation (1) is the
linearity, which basically means that the algebraic sum of two wave
functions is again a valid wave function subjected to Equation (1). This
property is also called the principle of superposition.
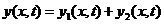
... (3)
Also, two kinds of boundary
conditions will be examined, namely, the fixed end and the free end.
These conditions decide shapes of reflected waves. Interference happens
when the incident and reflected waves overlap in the same region of the
medium. Moreover, standing waves are the interference formed when a
sinusoidal wave is reflected by the fixed end. In this case, there are
special points that never move at all called nodes. Midway between the
nodes are antinodes where the amplitude of motion is greatest. |
Instructions: 1.) To produce a single peaked pulse, give one end a small
upward shake or wiggle. The hand should move the rod up and then returns
once. 2.) To produce a sinosoidal wave, give the one end a repetitive, or
periodic up-and-down motion. 3.) To obtain a fixed end, use a clip to
give rigid support. 4.) Both ends are fixed when creating a certain
standing wave. So move a rod at desired antinodes gently up and down,
adjust the frequency and wait for the wave pattern to become steady. Pay
attention to those rods located at the positions of nodes.
PIC1: Black wave table

PIC2: Red wave table

|
Note to the Instructor: Move slowly in and out and comple all who see to touch. |
Possible CPS Questions:
1. Decide which of the following wave patterns
travels the fastest? [Question]
[Answer]
2. Agitate a pulse on each table at the same time.
Which pulse travels faster, knowing that iron rods are all the same
except lengths? [Question]
[Answer]
3. Agitate two pulses on both ends of red table at
the same time. What is going on after two pulses meet? [Question] [Answer]
4. What becomes the shape of a reflected wave? [Question] [Answer]
5. For standing waves on the red wave table what is
the minimal possible number of antinodes that can be realized? [Question] [Answer]
6. Wave equation (1) provides an excellent
description of motions on the wave table. Nevertheless, this does not
mean the imperfection, or more precisely, phenomena of non-linearity,
cannot be observed; for example, the sharp peak of a pulse may turn
flattened and widened. Decide which of the following factors contributes
to this fact. [Question] [Answer]
7. (Optional for interested students) When two wire
spines are joined, the coupled system can be used to demonstrate the wave
propagation through the boundary of two media with different wave speeds.
In this case, both reflected and transmitted (refracted) waves can be
observed. Does the frequency of wave change during this process? [Question] [Answer] |
|
Page created by
Xuefeng Zhang, Dept. of Physics & Astronomy, University of New Mexico |